PHOTOCHEMISTRY
Theoretical Concepts and Reaction Mechanisms
Yuri V. Il'ichev
Cordis Corporation, a Johnson and Johnson Company
P.O. Box 776, Welsh and McKean Roads, Spring House, PA 19477-0776
iilitche@its.jnj.com
1. Chemistry of Electronically Excited States
Aren't you excited already? Not yet? Let us then adopt a step-by-step approach in order to introduce you to a fascinating world of excited-state reactions. The term photochemistry generally applies to chemical modifications induced by interaction of light (electromagnetic radiation) with matter. Therefore, light is always one of the reactants in a photochemical system. Electromagnetic radiation with the wavelength ranging from ~800 nm (near-IR) to ~150 nm (far UV) is of primary importance for photochemistry and photobiology, but the wavelength regions adjacent to this range are also of interest for certain applications. With the advent of lasers, multiphoton photochemistry, i.e. chemistry initiated by simultaneous absorption of two or more photons, came into wide use. This made IR radiation of particular interests for photochemists. The wavelength range of 150-800 nm corresponds to the photon energy ranging from 800 to 150 kJ mol-1 (Figure 1).
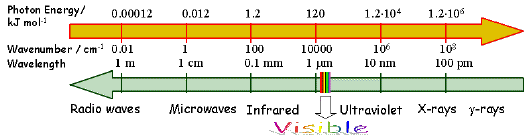
Figure 1. The electromagnetic spectrum.
These energies are much higher than those associated with thermal motion at ambient temperature and are comparable to the energies of chemical bonds. That is why photochemistry is often referred to as high-energy chemistry. The fact that the spectral region mentioned above contains electromagnetic radiation detectable by the human eye (visible light) suggests an interrelation of photochemistry and vision mechanisms. Humans can see radiation in this part of the spectrum because visual receptors are organic compounds that absorb light with these wavelengths. Notice that the spectral maximum of the solar radiation reaching the earth surface is located within the visible light range (~500 nm).
The basis for understanding light-matter interaction and chemical reactivity is quantum mechanics. According to this theory, a complete description of any molecular system can be provided by a function that is obtained upon solving the Schrödinger equation (a rather complex differential equation first introduced by Erwin Schrödinger). This function of multiple variables is called wavefunction. Generally, an infinite number of solutions (wavefunctions) with the corresponding values of the system energy are obtained from the Schrödinger equation. However, only some solutions with their characteristic values of the energy are physically acceptable. Thus, only certain values of the energy are allowed, although the number of these acceptable values can still be infinite. In other words, the energy of the molecular system is quantized.
Energy quantization is of primary importance for photochemistry, because it implies that only photons that bring a definite quantity of energy corresponding to a difference between two allowed energy values can be absorbed. The quantum mechanical results are conveniently illustrated by denoting discrete energy values according to a certain principle and plotting them on a graph with a vertical energy scale (compare to the Jablonski diagram in the module on Basic Photophysics). When a particular energy value, E, was designated with a certain symbol, e.g., S0, the system having the energy E is referred to as being in the state S0. Notice that this description may be incomplete because some systems may have the same energy, but be described by two different wavefunctions and, therefore, be in two different quantum states (this phenomenon is called degeneracy).
The application of quantum mechanics to molecular systems requires approximate methods because the Schrödinger equation cannot be solved exactly for many-body systems. Fortunately, nuclei are much heavier than the electrons, and consequently, their motion is much slower than that of the electrons. To a good approximation, the nuclei can be considered as fixed centers of potential and a description of the electronic motion can be obtained by solving the Schrödinger equation for a large number of different, but fixed nuclear positions. This way of separating electronic and nuclear motion is known as the Born-Oppenheimer approximation, or adiabatic approximation.
Generally, an infinite number of solutions (wavefunctions) with the corresponding electronic energies will be obtained for the electronic Schrödinger equation at each fixed nuclear configuration. The lowest electronic energy plotted against all internal variables (in general, 3N-6 for the system of N nuclei or 3N-5 for a linear N-atomic molecule) forms a multidimensional hypersurface corresponding to the ground state. This surface together with those corresponding to higher energies is referred to as the adiabatic potential energy surface. The electronic states are often designated according to the total spin (S or T for the singlet and triplet state with the spin 0 and 1, respectively, see also module on Basic Photophysics) and the relative energy (index "0" for the lowest energy, etc.). The majority of organic molecules are singlets in the lowest energy state, which is therefore referred to as the singlet ground state, or S0 state. Diatomic molecules have a single geometric parameter, internuclear distance, and therefore their potential energy surfaces reduce to curves. In this case a 2D-plot is sufficient for the presentation. Typical energy curves for the ground and first excited state are depicted in Figure 2.
Quantum mechanical treatment of nuclear motion within the Born-Oppenheimer approximation requires a solution of the nuclear Schrödinger equation with the electronic energy as the potential. Separation of different types of nuclear motion may often be achieved as a first approximation to complex molecular dynamics. This separation leads to several equations that are simpler than the original Schrödinger equation for the nuclei. There are three basic types of motion: translation, rotation, and vibration. Translation is the motion of the system as a whole, rotation is a motion in which the spatial orientation of the body changes, and vibration describe relative motion of the nuclei. Molecules moving freely in a macroscopic vessel may be treated as though their translational energy is not quantized. Another way of putting this is that the translational energy levels are so closely spaced that this type of motion may be well described with classical mechanics. Rotational and vibrational motion requires quantum mechanical treatment, which typically produces discrete energy levels such as shown in Figure 2.
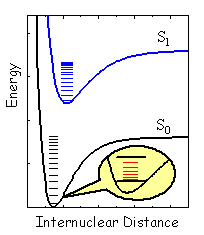
Figure 2. Potential energy curves corresponding to the ground state (black, S0) and first excited state (blue, S1) of a diatomic molecule. The states were assumed to be of singlet multiplicity. The energy levels for the vibrational motion are shown as black and blue lines inside the curves. Red lines in the insert show rotational levels for the the zero vibrational level of S0. Notice that characteristic energy for the rotational motion is much smaller than that for the vibrational motion, and the latter is much smaller than the energy associated with electronic motion.
The potential energy surfaces obtained by solving the electronic Schrödinger equation provide the basis on which chemical reactivity can be analyzed. It is a standard practice in photochemistry to define a common ground-state surface for all molecular species of the same stoichiometry. Minima on this surface can be identified with the equilibrium structures (all isomers and/or intermolecular complexes with the same formula). Statistical mechanics provides an answer to the question how properties of a macroscopic system are related to those of molecules constituting the system. The answer is given in terms of probabilities to find a molecule in a particular microscopic state or, in other words, in terms of the population of molecular energy states (see Boltzmann distribution in Basic Photophysics).
For the vast majority of molecular systems at any reasonable temperature only the ground electronic state is populated. Therefore, thermal chemistry is almost exclusively governed by the properties of the ground state. Notice that some excited vibrational states have typically non-zero population and most molecules are in the excited rotational levels at ambient temperature.
In contrast, photochemistry can only be understood if one considers properties of excited electronic states, which are typically populated by light absorption. These facts together with a fundamental understanding of the quantum nature of light provide the basis for interpreting photochemistry, not so much as high-energy chemistry, which utilizes light merely as an energy source, but more as reactivity of electronically excited species. These species can and often do exhibit chemical properties that are largely different from those of the ground-state species. Properties of S0 surface and the two lowest excited-state surfaces of different multiplicity, S1 and T1, are of primary importance for photochemistry.
2. Photochemistry Laws
The first law of photochemistry states that only the light absorbed by a molecule can produce photochemical modification in the molecule. Here and below, the term "molecule" is broadly defined and includes also atoms, radicals, etc. The law emphasizes the importance of light absorption by the molecule involved in the primary photoprocess, which is a chemical reaction or a physical process involving directly excited species. All aspects and consequences of this law must be considered for quantitative analysis of a photoreaction. This is generally taken for granted, but the frequent practice of comparing photochemical kinetic traces for different molecules without referring to their absorbance suggest that it is ignored more often than one may assume.
The second law of photochemistry was formulated at the beginning of 20th century when the quantum theory was just emerging. It states that one molecule is excited for each quantum of radiation absorbed. In other words, the absorption of light by a molecule is a one-photon process (see Figure 3). Therefore for a primary photoprocess only one molecule reacts for each photon absorbed. Typically several competing processes occur in the excited state. In this case, the second law can be reformulated as: the sum of the quantum yields (defined in Section 3, below) for the primary processes must be unity.
It has taken about 20 years and the development of quantum mechanics to predict two-photon absorption (Figure 3). The first experimental observation of the two-photon absorption was made when lasers were developed. Further development in laser technology made almost routine the generation of ultrashort light pulses (10-12 - 10-15 s). Such ultrafast lasers made possible not only experimental study, but also the broad application of multiphoton processes. Multiphoton fluorescence is widely used in imaging of cells and biological tissues. Multiphoton photochemistry recently received attention as a tool for time-resolved studies of important biological processes.
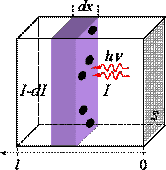
a b
Figure 3. (a) Schematic illustration of the light absorption by a rectangular sample. To a first approximation, molecules can be considered as opaque disks whose average cross-sectional area,, in cm2 molecule-1 represents the effective area that is impermeable for photons of a certain wavelength. We may consider an infinitesimal slab, dx, of a rectangular sample with a cross-section, S, which is equal to that of the light beam. The average intensity of light entering the slab is denoted I, and expressed in photon s-1. The intensity absorbed in the slab can be written as:
, where N is the concentration in molecule cm-3. Integrating this equation from 0 to l (sample length in cm) we obtain the Beer-Lambert law for one-photon absorption:
. If the concentration C is expressed in mol L-1 then the natural logarithm is usually substituted with the decimal one and the cross-section is replaced with the decimal molar absorptivity
.
Thus, we obtain:.
(b) Energy diagrams for one- and two-photon absorption. The average rate of n-photon absorption per molecule in photons s1 molecule-1 can be approximated as:, where
1 GM = 10-50 cm4 s photon-1 molecule-1. The unit was selected to honor Maria Göppert-Mayer who first predicted multiphoton absorption. The measured absorption rate Wn is the number of photons absorbed per s:, where Vex is the excitation volume. For one-photon absorption we obtain:
. This expression corresponds to the Beer-Lambert law limit for low absorption:
.
3. Photochemical Kinetics
Quantum yield is the major characteristics of a photochemical reaction. The quantum yield, also called the quantum efficiency, is defined as the number of events occurring per photon absorbed. These events might be related to physical processes responsible for energy dissipation (such processes are discussed in Basic Photophysics), but they also might be related to molecules of a chemical product formed upon photoirradiation. Generally, the (total) quantum yield of a photoreaction,
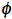, is:
(1)
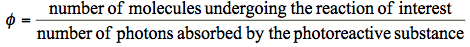
Eq. (1) would define the quantum yield of product formation,
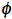p, if the number of product molecules would be determined. If the two numbers in Eq.(1) are measured per time and volume unit then the quantum yield is expressed in terms of rates (For more information on rate of reaction, see IUPAC Gold Book):
(2)
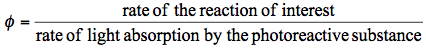
The latter quantity is also referred to as the differential quantum yield. Notice that these two definitions of the quantum yield agree only if the yield is constant during the course of the reaction. Eqs.(1) and (2) indicate that two separate measurements may be required to determine a quantum yield. In the simplest set-up, a reaction cell is mounted in a fixed position relative to the light source. The cell is charged with the sample of interest and irradiated. Photochemical conversion is determined with a suitable experimental technique (spectroscopy, chemical analysis, etc.). Afterwards, the cell is replaced with an actinometer, which is also irradiated. Before describing how actinometers work, it is important to say again that the amount of the radiation absorbed by the sample, rather than the total amount of light, has to be quantified.
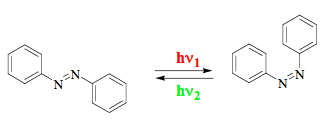
An actinometer is a physical device or chemical system, which is used to determine the number of photons in a light beam. Physical devices convert the energy of absorbed photons into another energy form, which may be easily quantified. The devices that operate by converting photon energy into heat represent 'primary' standards of actinometry. Other physical devices and chemical systems must be calibrated. Chemical actinometers are photoreactive mixtures with well-established photochemistry and known quantum yields. Two representative systems for liquid-phase actinometry are potassium ferrioxalate system and azobenzene system. In both cases, the photoconversion is monitored spectrophotometrically. It is interesting that the most frequently used ferrioxalate system has relatively complex chemistry. Its description in the textbooks hardly goes beyond the statement that Fe(III) is reduced and oxalate is simultaneously oxidized upon photoirradiation. In contrast, the photochemistry of azobenzene is extremely simple (Scheme 1). The isomerization reaction proceeds cleanly in both directions and the solution may be regenerated and reused many times.
A chemical reaction is just one of multiple routes to the loss of excitation. The light absorption produces an excited-state species that inevitably loses its energy through various deactivation mechanisms. To highlight essential features of photochemical kinetics, we will analyze the simplest system with multiple pathways of deactivation that are characterized by the rate constants corresponding to unimolecular irreversible processes. In the present context, a clear-cut distinction between photophysical processes and a single photochemical reaction will be made. It is assumed that one-photon absorption leads to the direct population of the reactive singlet excited state. The mechanism described corresponds to a scheme shown in Scheme 2.
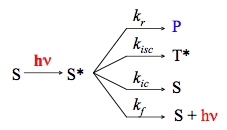
The rate constants kf , kic , and kisc refer to spontaneous emission, internal conversion and intersystem crossing, respectively. The rate constant kr corresponds to a chemical reaction. Assuming that population of S* by light absorption is characterized by the constant rate, W, in mol s-1, and the steady-state approximation (See IUPAC Gold Book) can be applied to the excited species we obtain the expression for the quantum yield of the photochemical reaction
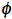0:
(3)
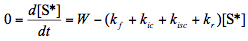
(4)
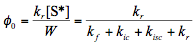
[Note: Eq.(3) was solved to obtain an expression for W, which was then used in Eq.(4).]
Quantum yields for the three other processes shown in Scheme 2 can be defined in the same way. Notice that the sum of all the quantum yields is equal to unity, as stated by the second law of photochemistry. The quantum yield for the photoreaction can be interpreted as the fraction of singlet excited molecules that undergo chemical transformation, i.e., the ratio of the number of molecules that react to the total number of S*. Because there always exists several routes to the loss of excitation, the quantum yield rather than the absolute rate constant must be used to compare the efficiencies of photochemical conversion for different reactive systems.
The steady-state approximation is inapplicable under conditions of time-dependent excitation. If a very short laser pulse is used to produce the excited species (so-called
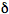-pulse excitation) the light absorption rate W can be neglected and Eq.(3) is easily integrated:
(5)
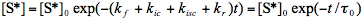
where
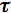0 is the observed lifetime of the singlet excited state.
(6)
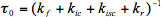
The observed lifetime is an average quantity defined for a large ensemble of the excited molecules. It can be measured with any experimental technique that is capable of detecting the excited species. To take an example, time-resolved fluorescence gives a convenient way of measuring
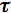0 provided that certain experimental conditions are fulfilled. Fluorescence detection relies on the photocurrent signal, which is linearly proportional, within certain limits, to the total number of photons emitted. The number of photons, in its turn, is proportional to the number of molecules in the singlet excited state, because individual molecules have time-independent probability to emit light. The fluorescence intensity measured as a function of time depends therefore on the concentration of S*, which is given by Eq.(5). In contrast to the observed lifetime, the radiative lifetime 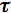f = 1/kf corresponds to the fluorescence decay rate in the absence of any other deactivation processes.
As mentioned above, light should be considered as one of the reactants in photochemical reactions. Therefore, 'effective concentration' of photons, which is given as the number of light quanta absorbed by the photoreactant, needs to be specified when one compares concentration-time profiles for photochemical conversion. In contrast, the efficiency of a thermal reaction can be visualized by plotting the normalized concentration of the reactant or product against time. To clarify this point we need to analyze the photochemical kinetics in more detail. According to the reaction scheme shown in Scheme 2, the rate of the product formation is:
(7)
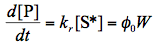
Inasmuch as concentrations are determined spechtrophotometrically, it is useful to rewrite Eq.(7) in terms of absorbances:
(8)
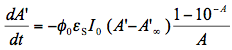
where
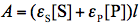and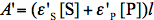 
refer to absorbance at the irradiation and observation wavelength, respectively. The absorbance, 
,
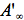is measured at the observation wavelength and infinite time, i.e., after complete conversion to the product. In the case of very weak absorption (A<<1), Eq.(8) is easily integrated and experimental data are linearized in the coordinates corresponding to the following equation:
(9)
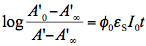
If we assume that the wavelength where only the reactant absorbs was selected for observation then absorbance in Eq.(9) can be replaced with the reactant concentration. Now a simpler equation, which looks very similar to the rate equation for the first-order thermal reaction can be obtained:
(10)
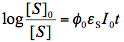
In contrast to thermal reactions, the proportionality coefficient
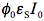in Eq.(10) is not just a rate constant independent of the initial concentration, but a complex quantity depending on three parameters. Therefore, the time dependence of the reactant concentration cannot be directly used to compare photoreactivity of different molecules, or even the same molecule if it was measured under different irradiation conditions. We could say that we need to know not only the reactant concentration but also effective 'light concentration',
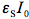, in order to analyze photochemical systems. Even if we use the same light source for two systems we cannot directly compare results unless we know how much light was absorbed by each system. Figure 4 shows simulated concentration profiles for two systems that realize the same photochemical reaction S --> P, but differ in spectral parameters and quantum yields. This plot shows how misleading could be a comparison of relative concentrations plotted against time for photochemical reactions if the system is not completely specified.
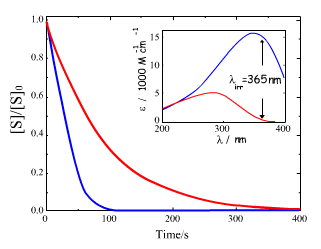
Figure 4. Time profiles for the normalized concentrations of two compounds undergoing an irreversible first-order photoreaction with a quantum yield of 0.1 and 1.0. Solutions containing these compounds at the same initial concentrations were irradiated with the same mercury lamp equipped with a 365 nm narrow-band filter. Which line, blue or red, corresponds to the molecule with the higher quantum yield (more photoreactive)? This question can only be answered when the absorbances at the irradiation wavelength are compared (see the insert for the absorption spectra). The substance corresponding to the blue curve has 60 times larger absorbance at 365 nm, which is responsible for faster conversion despite the 10 times lower quantum yield for its photoreaction. As to the question, the correct answer is that the red line corresponds to the molecule with the photoreaction quantum yield of 1.0. However, an extremely weak absorption at 365 nm results in a relatively slow phototransformation of this compound.
In a typical photochemical experiment the concentration of the excited species and transients (S* and T* in Scheme 2) is negligible in comparison to that of the ground-state species (S and P). Assuming that T* is not reactive and initially we have only the reactant at the concentration [S]0 we can write:
[S]0 ≈ [P]+[S].
Assuming that light absorption by all transient can also be neglected we can rewrite Eq.(7) as follows:
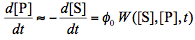
where W([S],[P],t) is the rate of light absorption by the reactant which is a function of time t and concentrations both the reactant and product. To obtain the expression for W we will use the Beer-Lambert law (Figure 3), and the fact the absorbances of components in a mixture add up together:
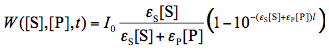
Here I0 is the intensity of monochromatic light entering the sample expressed in mol L-1s-1,
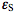and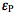 
are molar absorptivities of the reactant and product (M-1 cm-1), and l is the optical path (cm). The course of a photochemical reaction is often monitored spectrophotometrically at wavelength(s) different from the irradiation wavelength. By using the Beer-Lambert law we may write for the absorbance measured at the irradiation and observation wavelength at time t: 
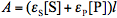and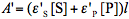 
. By using the absorbance, 
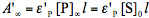, measured at the observation wavelength and infinite time and the three equations shown above we obtain Eq.(8). In the general case, Eq.(8) cannot be integrated. But it can be easily solved for very low and very high absorbance, and also for a special case when the product does not absorb at the irradiation wavelength, 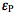= 0. In the later case we obtain:
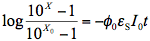
where
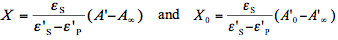
4. Theoretical Models of Photochemical Reactions
Within the Born-Oppenheimer approximation, potential energy surfaces govern nuclear motion and, therefore, chemical reactivity. However, in studying photochemistry it is also good to keep in mind that this is just an approximation, which is not automatically valid for all possible geometries and experimental conditions. A comprehensive picture of nuclear dynamics can be obtained from the time-dependent Schrödinger equation. However, a detailed account of nuclear motion can also be inferred from classical trajectories for a point moving without friction on the potential energy surface. The moving point may represent a chemically reactive system which consists of one or several molecular species. In the latter case one considers all reactants as a "supermolecule". The forces acting on the nuclei are given by minus the gradient of the potential (electronic energy) at this point. Recall that the gradient for a function of many variables is a vector formed by the first derivatives with respect to each of the variables.
Points on the surface that are characterized by the gradient vector of zero length are called stationary points. Their location is of primary importance for chemical reactivity. The nature of stationary points is determined by the secondary derivatives, the so-called Hessian matrix. If all the eigenvalues of this matrix are positive, the point is a minimum, which can be assigned to a reactant, product or intermediate. A first-order saddle point has all positive eigenvalues except for one, which is negative. It means that it is a maximum with respect to a single coordinate and a minimum in all other directions. Passage from one minimum to another one describes a chemical reaction and a saddle point between the two minima represents the transition state. Because of difficulties in representation of multidimensional hypersurfaces one-dimensional cross-sections through them are frequently used. The cross-sections may be compared to the potential energy curves of diatomic molecules and may often look similar to such curves. However, they must be interpreted with caution. For example, a saddle point may appear both as a minimum and maximum on two different cross-sections.
Thermal reactions are generally considered to be adiabatic, i.e., they are represented by the motion on the lowest potential energy surface. Another way of putting this is that these reactions occur exclusively in the ground state. Therefore, knowledge of the ground-state potential surface is sufficient for modeling thermal reactivity with reaction rate theories. In contrast, the theoretical treatment of any photochemical reaction requires information about potential energy surfaces for more than one state. The photoreaction starts from the ground state of the reactant(s), necessarily proceeds via electronically excited state(s), and ends with the product(s) in the ground state. Therefore, photochemical reactions inevitably include diabatic processes, i.e., a transition from one potential surface to another. This statement should illuminate the complexity of the theoretical analysis of photoreactions, especially because reliable calculations of the potential energy surfaces for electronically excited states of reasonably large molecules still represent a challenge for computational chemistry. Nevertheless, many fundamental aspects of complex photoinduced reactions still can be understood from qualitative analysis of potential energy surfaces.
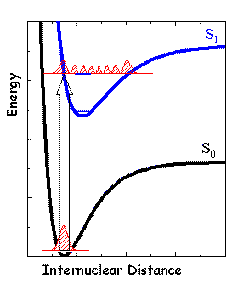
Figure 5. Franck-Condon Principle. The vibrational functions of two electronic states are approximately harmonic oscillator-like functions. The most probable position of the nuclei in the ground state corresponds to the maximum of the probability distribution function for the zero level (red curve). The energy gap between vibrational levels is usually large enough so that population of excited levels is small. An electronic transition caused by light absorption is represented by a vertical line (block arrow). The highest probability of the transition corresponds to the largest overlap between the ground-state and excited-state vibrational wavefunctions. The overlap is greatest for the S1 vibrational level whose classical turning point is near the equilibrium distance of the ground state.
Upon light absorption, a molecular system may be transferred from the ground state to an electronically excited state. According to the Franck-Condon principle, this transition tends to occur between those vibrational levels of two electronic states that have the same nuclear configurations. The time required for the absorption of a light quantum (~1 fs) is much shorter than a characteristic time of a nuclear vibration (~100 fs), and therefore, the nuclei cannot change their relative positions during the act of excitation. In other words, transitions between two potential energy surfaces can be represented by vertical lines connecting them (see Figure 5). In the course of a photochemical reaction there is a considerable time interval when the molecular system is out of the thermal equilibrium (a few ps in condensed phase, up to ms in low pressure gas phase reactions). It means that the population of vibrational energy levels may differ strongly from that predicted by the Boltzmann distribution (see Basic Photophysics). As a consequence of "vertical" electronic transitions and different equilibrium geometries of the ground and first excited state (Figure 5), immediately after excitation the molecular system will likely be in an excited vibrational state ("hot" molecule).
The amount of extra energy available for nuclear motion is a function of the excitation energy (wavelength). Vibrational excitation may also result from internal conversion or intersystem crossing, when electronic energy is converted into kinetic energy of the nuclei. It is known that internal conversion from S1 to S0 can be so fast in some systems that the thermal equilibration is first achieved only in the ground state. In solution, "hot" molecules in the first excited or ground state are quickly cooled down via interactions with the surroundings. Thermal equilibrium is normally established within a few picoseconds. Nevertheless this time is long enough to comprise several vibrational periods. The excess of kinetic energy may help the reactant(s) to overcome the barrier and relax into a new minimum. Chemical reactions of this type are called "hot". They preferentially occur in the gas phase at lower pressure where molecular collision frequency is much smaller than in the condensed phase.
We have already discussed that theoretical analysis of thermal reactions can be accomplished when minima and saddle points on the ground-state surface are allocated. The situation is much more complex for photochemical reactions. Difficulties emerge when one needs to explore several potential energy surfaces in detail. Luckily, only a few excited-state surfaces are of importance for the majority of photoreactions. Even so, topology of the three surfaces, S0, S1 and T1, which are almost without exception needed to understand the photoreaction mechanism, may be extremely complex. Minima on S1 and T1 surfaces may be anticipated in the regions near the ground-state equilibrium geometries and near geometries, corresponding to intermolecular complexes. The latter minima reflect much larger polarizability of excited species and therefore higher affinity to other molecules. Excited complexes can be formed from two molecules of the same type (excimer), or from two different molecules (exciplex). Return from the minima of these two types to the ground state usually does not produce a chemical change (Figure 6a) unless significant geometrical changes accompany the excitation and/or multiple close-spaced minima exist on the ground state surface (Figure 6b). Formaldehyde provides an example for large geometrical distortions in the excited state, the molecule is planar in S0, and pyramidal in S1 and T1.
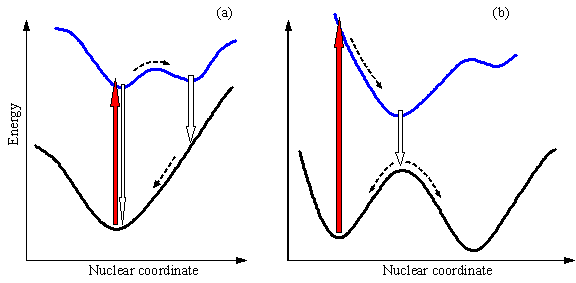
Figure 6. Schematic representation of the energy profiles corresponding to the ground state and the first excited state (a) for a system that undergoes an excited-state reaction but achieves no chemical conversion upon returning to the ground state and (b) for a system with partial conversion upon jumping to the ground state. Light absorption is represented by red block arrows, light emission by white block arrows.
In addition to localizing minima on the potential surfaces, finding the regions where the surfaces may cross or come very close to each other is of primary importance. The Born-Oppenheimer approximation is generally invalid in the vicinity of surface crossings and additional effects must be taken into account to describe the time evolution of the molecular species. The non-crossing rule states that potential energy curves can cross only if the electronic states have different symmetry (spatial or spin). Therefore the wavefunctions in the crossing region predicted by the simplest approximation has to be modified to avoid crossing of the potential energy curves (Figure 7). The non-crossing rule is strictly valid only for diatomic molecules. Intersection or touching of potential energy surfaces in polyatomic systems is generally allowed even if they belong to the states of the same symmetry. Recent studies showed that such crossing, also called conical intersection because of the topology of the surfaces at the crossing point, is quite common. The question whether a true conical intersection or avoided crossing is observed for a particular system of interest can be answered only with quantum mechanical calculations of high accuracy. These calculations recently became feasible for relatively large organic molecules, but reliable data are available just for a few systems.
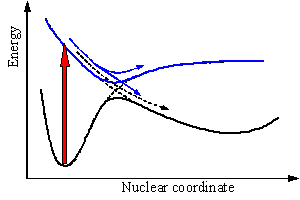
Figure 7. Adiabatic (solid) and non-adiabatic energy curves (dashed) for the S0 and S1 states. The light absorption is a vertical transition (block red arrow). Nuclear motion after excitation is governed by the S1 curve. Blue arrows show the motion in the case of avoided crossing and the black broken arrow corresponds to the allowed crossing.
Two hypothetical surfaces for the ground- and an excited state are depicted in Figure 8. The fact that multidimensional potential-energy surfaces may have numerous regions where they come very close to each other is of great importance for understanding photochemical mechanisms. First, non-radiative transitions such as internal conversion and intersystem crossing have much higher probability in these regions. Second, conical intersections (or weakly avoided crossings) serve as bottlenecks through which the photoreaction passes on the way from excited-state species to the ground-state products. In this sense crossing points are analogous to the transition states on the adiabatic surfaces. An essential distinct feature of the conical intersection is the presence of two independent pathways for the reaction (path f) as compared to the single path through the saddle point.
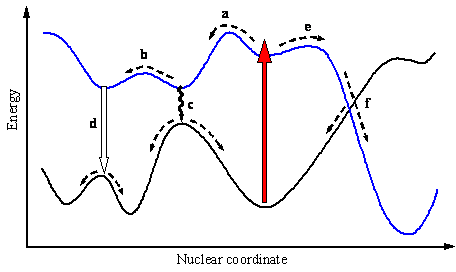
Figure 8. Potential energy surfaces of the ground and an excited state with various pathways (dashed lines) following the light absorption (red arrow).
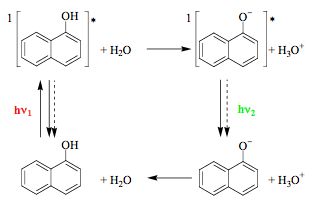
"Vertical" excitation typically leads to vibrationally excited species. Thermal equilibrium may be established during the lifetime of the excited state, meaning that vibrational relaxation takes place and the photoreaction starting from a minimum on the excited-state surface is said to have an excited-state intermediate (path a). Return from the first or even the second minimum reached on the excited-state surface often does not produce a new species (right part of path c) and the whole sequence may be considered as a photophysical process. A typical example is the protolytic dissociation of 1-naphthol in the singlet excited state (Scheme 3). The acidity of this molecule increases dramatically upon excitation (pKa = 9.2 and 0.4 for S0 and S1) and proton is transferred to a suitable acceptor such as water. It has to be noted that Scheme 3 does not account for all photoprocesses occurring in
1-naphthol solutions.
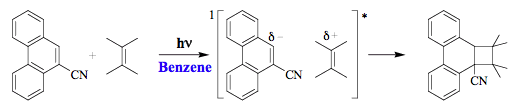
The primary excited-state intermediate in Figure 8 may produce a new molecule in the excited state, which undergoes further modifications (path b), or returns to a new minimum on the ground-state surface (left part of path c). A jump from the excited-state surface can be accomplished via non-radiative transition (path c) or light emission
(path d). An illustrative example of an excited-state intermediate in the photochemical reaction is the interaction of 9-cyanophenathrene with tetramethylethene in benzene that forms a cycloadduct via a singlet exciplex (Scheme 4).
The reaction sequences represented by motion on the excited-state adiabatic surface are usually called adiabatic reactions. If the loss of excitation occurs anywhere on the reaction path between the points corresponding to reactants and products, then such photoreaction may be referred to as diabatic (also called non-adiabatic). It is also possible that the vibrational relaxation first occurs in the ground state (path e in Figure 8). Such a photoreaction is called "direct". A direct reaction proceeds through a funnel (path f), which is a region of the potential energy surface where the probability for a jump from one energy surface to another one is very high. Funnels usually correspond to conical intersections or weakly avoided crossings. To characterize a molecule in a funnel one needs not only the positions of the nuclei but also their velocity vectors. In some systems passage through a conical intersection may also be separated from the excited-state minimum initially populated by a small barrier (paths a and c assuming that surfaces now cross at the point corresponding to path c). The presence of a S1-S0 conical intersection separated from the "vertical" geometry by a small barrier has been predicted for benzene. This funnel is responsible for the opening of efficient deactivation channel leading to disappearance of fluorescence and isomerization (Scheme 5) when the benzene molecule has enough vibrational energy to overcome the barrier.
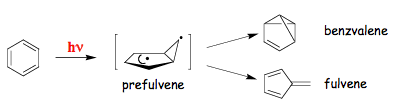
5. Factors Determining Outcome of a Photochemical Reaction
The wide variety of molecular mechanisms of photochemical reactions makes a general discussion of such factors very difficult. The chemical nature of the reactant(s) is definitely among the most important factors determining chemical reactivity initiated by light. However, a better understanding of this aspect may be gained from a closer examination of the individual groups of chemical compounds. The nature of excited states involved in a photoreaction is directly related to the electronic structure of the reactant(s).
Environmental variables, i.e., parameters that are not directly related to the chemical nature of the reacting systems, may also strongly affect photochemical reactivity. It is useful to distinguish between variables that are common for thermal and photochemical reactions, and those that are specific for the reactions of excited species. The first group includes reaction medium, reaction mixture composition, temperature, isotope effects to name the most important. The distinctive feature of photochemical reactions is that these parameters almost always operate under conditions when one or more photophysical processes compete with a photoreaction. The result of a photoinduced transformation can only be understood as the interplay of several processes corresponding to passages on and between at least two potential energy surfaces. We saw that even the simplest system, shown in Scheme 2, corresponds to parallel reactions in terms of reaction kinetics.
Reaction medium may directly modify the potential energy surfaces of the ground and excited states and hence affect the photoreactivity. The outcome of the two reactions presented in Schemes 3 and 4 changes dramatically when solvent polarity and hydrogen bonding capacity are changed. The protolytic photodissociation of 1-naphthol is completely suppressed in aprotic solvents because of unfavorable solvation energies both for the anion and proton. Under such conditions, proton transfer reaction cannot compete with the deactivation. The formation of two new products (Scheme 6) in the reaction of 9-cyanophenathrene with tetramethylethene is observed in methanol, because the exciplex dissociated into radical ions. It means that the potential energy minimum corresponding to the ion-radical pair shifts below that of the exciplex in polar solvents. The ion-radical formation is often followed by proton transfer reactions.
Solvent viscosity will strongly affect photoreactions where the encounter of two reactants or a substantial structural change are required. In highly viscous or solid solutions the loss of excitation via light emission or unimolecular non-radiative deactivation is more probable than a chemical modification of the excited species. On the other hand, slow diffusion in viscous solutions may prevent self-deactivation of the triplet state via a bimolecular process called triplet-triplet annihilation and enhance the efficiency of a photoreaction from this state. Triplet-triplet annihilation belongs to electronic-energy transfer processes, which may be classified as quenching of excited states. Quenching rate is a very important factor in discussing effects of medium and reaction mixture composition on photoreactivity. Quenching of excited states is a general phenomenon that is realized via different mechanisms. Any process that leads to the disappearance of the excited state of interest may be considered as quenching. In general it can be represented as:
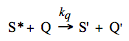
Notice that the quencher molecule Q may belong to the same kind of chemical species as the excited molecule, and be either in the ground or in an excited state. S' corresponds to the ground state or to an excited state of lower energy. For the purpose of our discussion we separated quenching described by Scheme 7 from all other processes, including the photoreaction of interest introduced in Scheme 2. Obviously, this separation is just a matter of convention. Generally, any chemical reaction of the excited species can be considered as a quenching process for fluorescence. Scheme 7 can easily be incorporated into the reaction scheme (see Scheme 8) and into our kinetic analysis as an additional pseudo-unimolecular rate constant kq[Q].
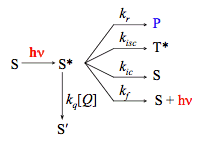
Scheme 8. Kinetic scheme for a simple system with a photoreactive singlet state in the presence of a quencher.
In the presence of a quencher, Q, the observed lifetime of the excited molecule and therefore the quantum yield of the photoreaction may be significantly reduced.
(11)
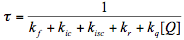
(12)
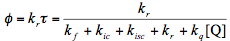
Eq. (4), (6), (11), and (12) can be combined into a single one:
(13)
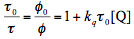
where index "0" refers to the system without quenching. If we would consider the fluorescence quantum yield instead of the photoreaction yield, we would obtain a similar equation, which is known as the Stern-Volmer equation. The mechanism just considered corresponds to so-called dynamic quenching that results purely from encounters between excited molecules and the quencher. It is also conceivable that Q and S form a ground-state complex, which has a different reactivity and/or does not fluoresce. This situation is referred to as static quenching. In the case of static quenching, the quantum yield is diminished but the observed lifetime remains constant. In any event, the existence of quenching emphasizes the importance of the concentration as a controlling factor in photochemistry. For many systems, the quenching rate constant, kq, is close to the diffusion-controlled limit which is of the order 1010 M-1s-1 at ambient temperature in liquid solutions. It means that quenching effects may become noticeable at the quencher concentrations > 1 mM and > 1 µM for the singlet state and triplet state with characteristic lifetimes of 10 ns and 10 µs, respectively. Thus even minor impurities may cause photoreaction quenching. The concentration of the photoreactive compound S may also play an important role if self-quenching takes place.
Because of the energy conservation law the excitation energy in a quenching process must be either dissipated in the form of thermal energy, or accumulated in the form of chemical energy of the quenching products or transferred to the quencher Q. According to these three possibilities one may distinguish physical mechanisms of quenching from chemical ones and from energy transfer. However, a clear cut is not always possible or worth making. The formation of excimers is frequently observed in solutions of aromatic hydrocarbons, such as anthracene or pyrene. The potential energy surfaces in these systems frequently look similar to that shown in Figure 6a. Thus, the entire reaction sequence leads only to quenching of the excited monomer. The quenching will be seen in a reduced quantum yield of the monomer fluorescence and a monomer photoreaction. An illustrative example is
1-hydroxypyrene, which is a moderately strong photoacid in water. In the singlet excited states it readily transfers a proton to a suitable base such as acetate anion (analogous to the reaction shown in Scheme 3). But at higher concentrations of 1-hydroxypyrene, the quantum yield of the photoinduced proton transfer decreases because of the formation of the excimer, which is not as efficient as the proton donor. Exciplexes are typically more reactive, and provide examples for combined physical and chemical quenching (see Schemes 4 and 6).
Fluorescence self-quenching in aqueous solutions of dyes, such as fluorescein or eosin, has been known for more than 100 years. Several mechanisms involving collisional quenching, ground-state aggregation and energy transfer to the aggregates has been proposed to account for this phenomenon. In principle, quenching by the ground state could be observed for almost every excited species under conditions favoring the close proximity of two molecules. That is why it is often reported for systems with confined geometries such as those of surfactant assemblies. There exist many examples of self-quenching of the triplet state that plays a role in photochemistry. For example, the quenching of anthrone triplets by its ground state in benzene occurs with a rate constant close to 109 M-1s-1 and results in the formation of two radicals (Scheme 9). The photoreactivity of 10,10-dimethylanthrone differs dramatically, because methyl substituents prevent the reactive self-quenching.
Compounds with heavy atoms and paramagnetic species increase the rate of intersystem crossing. It has to be emphasized that such molecules enhance the efficiency both of the S1 --> T1 and T1 --> S0 transitions, and should be considered as quenchers both for singlets and triplets. The yields of photochemical reactions originating from the singlet excited state, as a rule, are adversely affected by these quenchers. In contrast, the efficiency of photoconversion from the triplet state is usually increased because the triplet lifetime remains sufficiently long in the presence of a quencher, and the overall effects is largely determined by an increase in the yield of the triplets. An example is given by the photoreaction of anthracene with 1,3-cyclohexadiene which mainly forms product A (Scheme 10). In the presence of methyl iodide (iodine is a heavy atom), the major product is compound B, which was also obtained in small quantities in the absence of the quencher. The results suggest that B is formed in a triplet-state reaction.
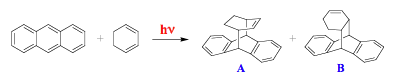
The most important paramagnetic species is molecular oxygen, which is known to be very efficient quencher of excited states. Quenching by O2 is particularly important for the triplet state because of its long lifetime (see Eq.(13)), so that even traces of oxygen may strongly affect photoreaction occurring through the triplet state. The ground state of O2 is a triplet state. The first singlet excited state is only 22 kcal mol-1 above the ground state. This energy corresponds to near-IR radiation with a wavenumber of 7882.4 cm-1 or wavelength of 1269 nm. Singlet oxygen is a reactive species interacting with a wide variety of substrates. It can be generated using dyes with a high triplet yield, such as rose bengal or methylene blue. As mentioned above this process belongs to the type of quenching that is called electronic energy transfer.
The outcome of an energy-transfer process is the quenching of the luminescence or photoreaction associated with the donor and the initiation of the luminescence or photoreaction characteristic of the energy acceptor. The subsequent reactions of the acceptor are said to be sensitized. Electronic energy transfer can be described by Scheme 7, where Q' has to be an excited-state species. Two general mechanisms of the energy transfer are distinguished: radiative and nonradiative. The radiative mechanism, often described as "trivial", is realized through the emission of light by the donor, and its absorption by the acceptor. Nonradiative energy transfer is a single-step process that requires the direct interaction of the donor and acceptor.
The specific variables of any photoreaction, as compared to thermal chemical processes, are the wavelength and intensity of excitation light. Wavelength dependence of the quantum yield or photoproduct composition may result from the occurrence of "hot" reactions or reactions from higher excited states (S2, T2, etc.). The latter processes have to be extremely fast to compete with internal conversion, which is typically accomplished within 1 ps. The presence of slowly inter-converting conformers or isomers with different absorption spectra may also cause wavelength-dependent photoreactions.
The intensity of excitation light is the key to multi-photon photochemistry (see legend to Figure 3). Because of the n-th power dependence of the absorption rate the photoreaction may become detectable only when the photon flux is above a certain threshold value. In one-photon photoreactions, primary processes are normally not affected by the light intensity. However, the overall reaction might be very sensitive to it, because relatively long-lived intermediates may come into play. These intermediates may absorb light and undergo photochemical reactions, or be involved in bimolecular reactions (e.g., triplet-triplet annihilation) that are strongly dependent on their concentration, and therefore light intensity.
6. Exciting World of Photoreactions
There exist a plethora of photoreactions practically for each class of chemical compounds. These reactions may be categorized according to chemical composition and structure. They may also be classified under different types by using theoretical models for the description of the excited state(s) or structure of the potential energy surface. However, for our introductory discussion it seems to be more appropriate just to consider some examples classified by general reaction types (Figure 9).
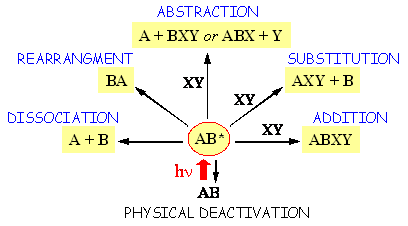
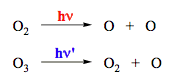
Considering the high energies involved in electronic excitation, photoinduced dissociation may be expected as a typical reaction pathway. However, photodecomposition via dissociative pathway(s) is not so common in photochemistry, particularly for large molecules in solution. This can be easily understood if one recalls that electronic excitation is usually not localized in a particular vibrational mode, and primary products of the dissociation have a high probability to recombine, because of cage effects. In solution, two fragments of a molecule are trapped within a "cage" of solvent molecules, and undergo numerous collisions before they escape the cage. Dissociative processes play a much more important role in gas-phase photochemistry. The photodissociation of small molecules driven by the UV radiation is of profound importance for atmospheric photochemistry.
Photodecomposition of O2 and O3 (Scheme 11) may afford the products in different electronic states depending on the excitation wavelength. These processes participate in establishing peculiar profiles for atmospheric temperature and the solar radiation spectrum on the earth surface. The gas-phase photoionization (removal of an electron) also belongs to dissociation reactions. The reactions shown in Scheme 12 may occur in the upper atmosphere due to short-wavelength UV radiation from the Sun.
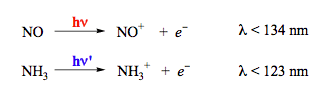
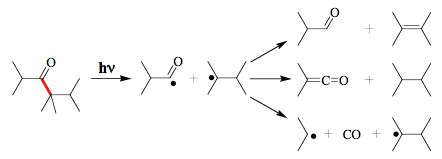
An important primary photoprocess of carbonyl compounds is
cleavage, also known as a Norrish Type I reaction (Scheme 13). Besides recombination, the acyl and the alkyl radicals formed in the primary reaction can undergo numerous secondary reactions that are responsible for the multitude of final products.
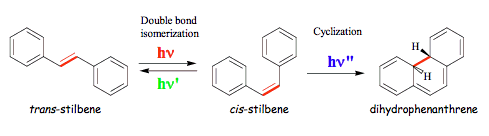
Rearrangements of electronically excited molecules present one of the most exciting chapters in photochemistry in the sense that they follow reaction pathways that are usually inaccessible for the ground state (activation barriers in the ground state are very high). The cis-trans isomerization of double bonds belongs to such reactions. The azobenzene reaction depicted in Scheme 1 provides an instructive example. Scheme 14 shows photoinduced rearrangements of stilbene that has been extensively studied. In addition to double bond isomerization, cis-stilbene undergoes also cyclization with a lower quantum yield to form dihydrophenanthrene. The cis-trans isomerization of stilbene occurs through rotation around the double bond. In the ground state this rotation encounters a large barrier, i.e., there is a maximum on the ground-state potential energy surface at the geometry corresponding to a twist angle of about 90o. In contrast, both the first singlet excited state and triplet state have a minimum approximately at the same geometry. The close proximity of the minimum and maximum facilitates a jump to the ground state (compare to path c in Figure 8). The cis-trans isomerization of azobenzene may proceeds not only through rotation, but also through nitrogen inversion, i.e. in-plane motion of the phenyl ring.
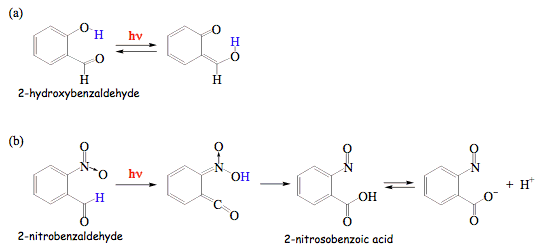
Two illuminating examples of photoinduced rearrangements of substituted benzaldehydes are presented in Scheme 15. Intramolecular hydrogen transfer in 2-hydroxybenzaldehyde is an extremely fast reaction in the singlet excited state. However, the process is completely reversed upon a jump to the ground state. Overall, no chemical conversion is observed and excitation energy is either dissipated as heat or emitted as light, but with a longer wavelength (see Figure 6a). This behavior is typical for aromatic carbonyl compounds with ortho-hydroxy groups, and they found application as UV protectors, in sunscreens for example. Molecules acting as UV protectors absorb light that is harmful for biological molecules, and convert light into heat or radiation that is biologically benign. In contrast, an intramolecular hydrogen transfer in
2-nitrobenzaldehyde initiates a sequence of the ground-state reactions that leads to 2-nitrosobenzoic acid. The latter molecule is a moderately strong acid, and dissociates in aqueous solutions so that the photochemistry of 2-nitrobenzaldehyde can be used to create a rapid pH-jump in solution. Many biological macromolecules, such as proteins and nucleic acids, show pH-dependent conformational changes. Those changes can be monitored in real time by using the light-induced
pH-jump.
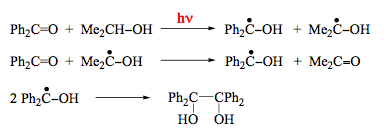
Scheme 9 gives an example of photoinduced abstraction. The two reactions shown in Schemes 3 and 6 can also be classified as abstraction reactions. Here, a proton or an electron is abstracted from the excited molecule by the ground-state species. These processes, often combined under the term "charge-transfer reactions", play an important role in many photoinduced processes. Excited-state electron transfer constitutes a decisive step in the entire process of photosynthesis. Hydrogen atom abstraction reactions are known for more than 100 years and belong to the most extensively studied photoprocesses. The reaction of benzophenone in the triplet excited state with isopropanol provides another example for this type of photoreactions (Scheme 16). The dimethylketyl radical produced transfers a hydrogen atom to benzophenone in the ground state to produce another diphenylketyl radical. It is interesting that only one photon is needed to convert two molecules of the reactant and the quantum yield of benzophenone decomposition has a limiting value of 2.
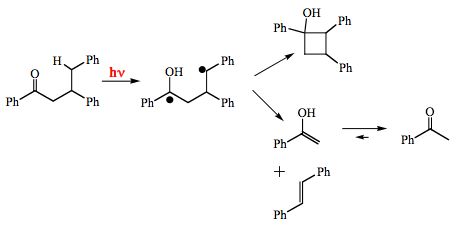
Intramolecular hydrogen abstraction is a common photoreaction of carbonyl compounds with a hydrogen atom attached to the fourth carbon atom (Scheme 17). The resulting diradical can form cycloalkanol or undergo C-C bond fission to give an alkene and enol. The latter is usually thermodynamically unfavorable and converts to a ketone. Intramolecular abstraction of a
-hydrogen is known as a Norrish Type II process.
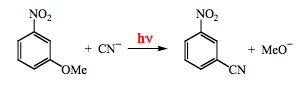
Photosubstitution reactions are well characterized for substituted aromatic compounds. An illustrative example is the photoreaction of m-nitroanisole with cyanide ion (Scheme 18). The mechanism involves a complex of the aromatic molecule in the triplet state with the nucleophile.
A photohydrolysis reaction in aqueous solution (substitution with OH-) was utilized to provide the rapid light-controlled release of biologically active molecules, such as aminoacids, nucleotides, etc. Biologically inert compounds affording such release upon photoirradiation are referred to as "caged" compounds. Two-photon photochemistry is of great interest for such studies, because one can utilize red light or IR radiation, which is not absorbed by biomolecules, and is biologically benign. The two-photon photohydrolysis of the glutamate ester of hydroxycoumarin (Scheme 19) is characterized by a reasonably high cross-section for two-photon absorption.
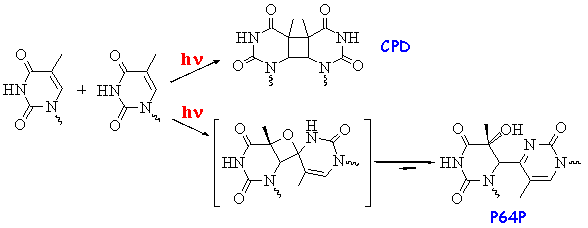
Addition reactions are quite common among electronically excited molecules. An example of cycloaddition occurring both from the singlet and triplet excited state is shown in Scheme 10. Photoinitiated cycloaddition reactions are of great importance for understanding the mutagenic effects of UV radiation. Two major photolesions produced in DNA by UV light are cyclobutane pyrimidine dimers (CPD) and pyrimidine(6-4)pyrimidone adducts (P64P) (Scheme 20). These lesions are thought to represent the predominant forms of premutagenic damage. Generally, the overall yield of P64P is substantially lower than that for CPD, but CPD was found to be less mutagenic than the P64P adduct. CPD is formed in cycloaddition involving excited thymine or cytosine and another pyrimidine nucleobase in the ground state. The proposed, but still not proven mechanism for the P64P formation includes an unstable intermediate with a 4-membered ring, which undergoes fast H-transfer and ring opening.
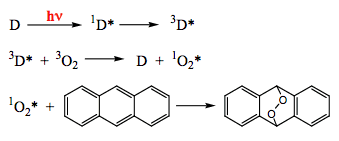
The addition of singlet oxygen to double bonds is well known. Because singlet oxygen can be generated photochemically via energy transfer, the entire reaction sequence, such as shown in Scheme 21, provides an example of sensitized addition photoreaction.
7. Supplemental Reading
Barltrop, J.A., Coyl, J.D. (1975) Excited states in organic chemistry, London ; New York: Wiley, 1975, 376 p.
Klessinger, M., Michl J. (1995) Excited states and photochemistry of organic molecules, New York: Wiley-VCH Publishers, 538 p.
Michl, J., Bonacic-Koutecky, V. (1990) Electronic aspects of organic photochemistry, New York: Wiley, 475 p.
Turro, N.J. (1991) Modern Molecular Photochemistry, Sausalito: University Science, 628 p.
Wayne, C.E., Wayne, R.P. (1996) Photochemistry, Oxford: Oxford University Press, 96 p.
10/20/08
02/02/09