SYSTEMS BIOLOGY of PHOTOSYNTHESIS
Xin-Guang Zhu
Plant Systems Biology Group, Institute of Computational Biology,
Chinese Academy of Sciences/Max Planck Society, Yue Yang Road,
Shanghai, China, 200031
zhuxinguang@picb.ac.cn
www.picb.ac.cn/~zhuxinguang
Translated into Macedonian
Translated into Portuguese
Translated into Estonian
Translated into Croatian
Translated into French
Introduction
With the depletion of fossil fuels and the growing demand for food production, plant biologists for the first time in history are playing a major role in solving a grand challenge for the society, i.e., identifying new ways to increase plant productivity under a changing global climate. Increasing photosynthetic energy conversion efficiency is one major route still available for us to dramatically increase crop productivity. Combining systems models with an evolutionary algorithm provides one efficient and feasible mechanism to identify new approaches to engineer higher photosynthesis.
Much of our knowledge about photosynthesis is gained through a reductionist's approach, where each individual component of the system is isolated and studied independently. Through this approach, we have obtained detailed biophysical and biochemical information about different components of photosynthesis. At the same time, modern biotechnology enables easy up or down regulation of nearly every gene in photosynthesis. Even with all these capacities and knowledge, we are still very far from being able to precisely engineer the photosynthetic apparatus for a higher photosynthetic rate. This is not too surprising considering that the photosynthetic energy conversion efficiency is a systems property, i.e., it is determined by the interaction between different components of the systems, not determined by any individual component of the system.
Given that photosynthesis is the basis of both food and energy production and the increased demand for both in our society, how can we engineer higher photosynthesis? In other words, what is limiting photosynthesis for different plants under different environments? The answers to these two questions holds the key to increasing plant productivity. Answering these two questions are extremely challenging. More than one hundred proteins are involved in photosynthesis. Even if manipulation is limited to simply altering the amount of protein, rather than its properties, the potential permutations will run into the millions.
Considering that multiple proteins might need to be engineered at the same time, it quickly becomes apparent that experimentally up-regulating or down-regulating the amount of each protein and examining its impacts on productivity is inefficient. One potential way to solve this problem is to take a systems approach. The systems approach is to develop mathematical models, which can faithfully simulate all of the biophysical and biochemical processes involved in photosynthesis, then, to conduct numerical experiments to identify targets to engineer for higher productivity.
I will use a model of photosynthetic carbon metabolism to illustrate the basic methodology of developing systems models, and using an evolutionary algorithm to identify the optimal nitrogen allocation in metabolism for a higher photosynthetic rate of CO2 uptake. I will also briefly describe the other major applications of systems models of photosynthesis, which include linking genomic data to physiological data, studying dynamic signals in photosynthesis, studying the significance of changes in the photosynthetic apparatus to increase photosynthetic efficiency, and working as the basis for ecophysiological models.
One of the key targets for plant biology research is to increase photosynthesis
During the past four decades, plant breeding has produced remarkable increases in the potential yields of many crops. Potential yield is defined as the yield that a genotype can achieve without biotic and abiotic stresses. Following the principles of Monteith (1977), the potential yield (Y) of a crop and primary production (Pn) at a given location is determined by:
Pn = St.εi. εc/k .... (1a)
Y = η.Pn .... (1b)
Where St is the annual integral of incident solar radiation (MJ m-2), εi the efficiency with which radiation is intercepted by the crop; εc the efficiency with which the intercepted radiation is converted into biomass; η the harvest index or the efficiency with which biomass is partitioned into the harvested product; and k the energy content of the plant mass (MJ g-1). St is determined by the site and year. k varies very little between vegetative organs, typically averaging 17 MJ/kg, though grain with significant oil content may have higher energy contents (Roberts et al., 1993). Pn is the primary productivity, i.e., the total plant biomass produced over the growing season. Based on Equation 1, Y is determined by the combined product of three efficiencies, each describing broad physiological properties of the crop: εi, εc, and η. ε1 is determined by the speed of canopy development and closure, and canopy longevity, size and architecture. εc is a function of the combined photosynthetic rate of all leaves within the canopy, less crop respiratory losses (Long et al., 2006).
In the context of Equation 1, increases in potential yield over the past 40 years have resulted largely from an increase in η and εi, whilst realized yields have been improved through better fertilization and improved disease protection, in turn increasing εi (reviewed: Long et al., 2006). But, how can we increase Y further? Healthy crops of modern cultivars at optimized spacing intercept most of the available radiation within their growing season, limiting prospects for improving εi. Grain in the modern cultivars of cereals can represent 60% of the total biomass at harvest (Evan, 1993). The harvest index for grain appears to be approaching an upper limit, given that a minimum quantity of biomass must remain in the plant body, to ensure that vital nutrients and reserves can be translocated into the grain, and to account for cell wall materials that cannot be degraded. The harvest index for biomass crops is even higher. If η and εi are approaching an upper limit, further increase in potential yield can only be achieved by an increase in εc, which is determined by photosynthesis and respiration.
So, what is the theoretical maximal εc, and what is the realized εc? A theoretical analysis suggest that the maximal εc for C3 and C4 plants are 4.6% and 6%, respectively (Figure 1, see details of the calculation in Zhu et al., 2008).
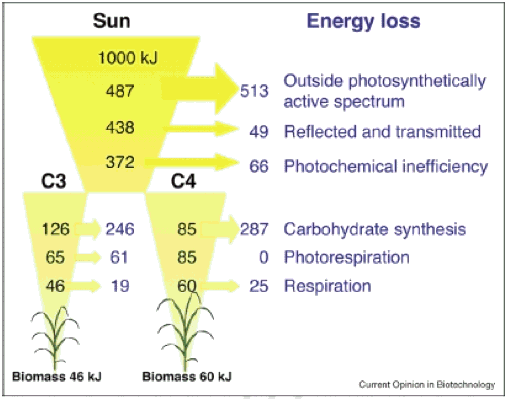
Figure 1. Minimum energy losses calculated for 1000 kJ of incident solar radiation, at each discrete step of the plant photosynthetic process from interception of radiation to the formation of stored chemical energy in biomass. Both C3 and C4 (NADP-Malic Enzyme type) photosynthesis are considered. Calculations assume a leaf temperature of 30°C and an atmospheric [CO2] of 380 ppm. The arrows indicate the amount of energy losses for different processes (Zhu et al., 2008).
For C3 crops, the highest short-term efficiencies are about 0.035, and for C4 about 0.043; the commonly achieved εc in the field is only about 1/3 of these maximal values, suggesting that there is substantial room available to further increase εc (reviewed in Zhu et al., 2008). Direct evidence was provided by plants grown under Free Air CO2 Enrichment, where both photosynthetic rate and plant productivity are increased (Long et al., 2004).
How can we identify new ways to engineer for higher productivity? As discussed earlier, experimental approaches become inefficient in identifying new engineering targets. Here I will use the model of photosynthetic carbon metabolism to illustrate a systems approach to identify new targets to engineer higher photosynthetic energy conversion efficiency.
Systems biology approach to identify new opportunities to engineer for higher productivity
In this section, I will briefly describe the basic procedure for developing a systems model, and then describe the method of combining the systems model with evolutionary algorithms to identify new targets to engineer for higher productivity. At the end of this section, I will explain why evolution has not selected the optimal photosynthetic apparatus.
i) The basic procedure to develop a systems model
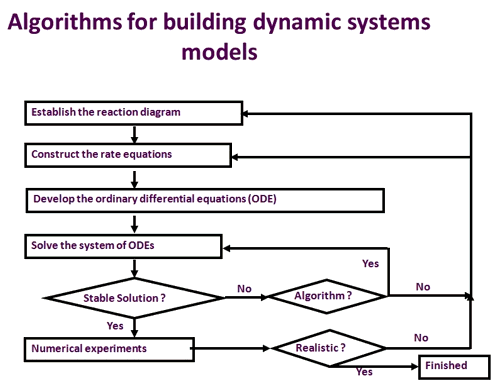
Figure 2. The general algorithm to build a dynamic systems model. The process involved in the development of a systems model includes establishing the reaction diagram, building the rate equations, building the ordinary differential equations, testing and validation of the model results with experimental observations. This process iterates until the model can faithfully reproduce commonly observed responses to genetic or environmental perturbations.
Figure 2 illustrates the process used to develop a kinetic model of the metabolic process. First, the reactions closely involved in this process need to be compiled to form a reaction diagram. Then, the rate equation for each reaction involved in the diagram is developed. A systems model representing this metabolic process is then constructed by developing an ordinary differential equation (ODE) for each metabolite involved in the process. Each ODE describes the rate of change of the metabolite concentration with time, formed by rates of formation minus the rate of consumption of this metabolite. For example, in photosynthetic carbon metabolism , RuBP (Ribulose-1,5-bisphosphate) is formed through Ru5P (Ribulose-5-phosphate) phosphorylation via the reaction:
Ru5P+ATP→ ADP + RuBP …. 2
It is consumed via both RuBP carboxylation and RuBP oxygenation:
RuBP + CO2 → 2 PGA …. 3
RuBP + O2 → PGA + PGCA …. 4
where PGA is 3-phosphoglycerate and PGCA is 2-phosphoglycollate. Assuming that the rate of RuBP phosphorylation is vrp and the rates of RuBP carboxylation (Equation 3) and oxygenation (Equation 4) are vc and vo, respectively, then the rate of RuBP concentration change with time is expressed as:
d[RuBP]/dt = vrp-vc-vo …. 5
All ODEs collectively form a system of ordinary differential equations, the solution of which corresponds to different physiological and dynamic states of metabolic process.
Once a system of ordinary differential equations has been constructed, a series of numerical experiments are required to test and validate the model. Normally, a systems model has to show its ability to gain steady states, robustness against external perturbation, and the ability to predict commonly observed phenomena. For example, the model of photosynthetic carbon metabolism reached a steady state within about 200 seconds (Zhu et al., 2007). It faithfully simulated the commonly measured A-Ci curve, i.e., the CO2 uptake versus intercellular CO2 concentration (Ci) curve, for both normal (21%) and low (2%) oxygen levels. Furthermore, after a drastic perturbation of the intercellular O2 concentration, the model can quickly regain a new steady state with a realistic rate of photosynthesis. Finally, the model faithfully simulated phosphate limited photosynthesis under conditions of a low rate of triose phosphate utilization (Zhu et al., 2007). After these validations, the photosynthetic carbon metabolism model can be used to identify new targets to engineer higher photosynthetic efficiency.
ii) Combining systems model with evolutionary algorithm to identify new targets to engineer for higher productivity
In traditional breeding, crosses between different plants create variations in certain traits, such as crop yield. Seeds for those individuals with superior trait quality are selected and used to generate individuals for the next generation. After many generations, the selected traits are gradually improved during this process. This method led to a dramatic increase in crop productivity, and created the "green revolution". Analogous to the selection of better traits over generations in traditional breeding, combining systems models with an evolutionary algorithm enables a simulated evolution of the photosynthetic apparatus for a higher photosynthetic rate.
The evolutionary algorithm essentially mimics the process of natural selection. In real natural selection, the selection pressure is to ensure survival and higher fecundity. In the artificial selection mimicked by the evolutionary algorithm, the selection pressure is to have a higher photosynthetic CO2 uptake rate with the same amount of nitrogen investment in the enzymes in photosynthetic carbon metabolism. Furthermore, each generation has many individuals, with each individual representing one set of enzyme concentrations required to run the model of carbon metabolism. For each individual, or set of enzyme concentrations, there is one steady-state rate of CO2 uptake. In each generation, the individual with a higher photosynthetic CO2 uptake rate will be selected to "seed" the next generation. To generate individuals for the next generations, the selected individual will be duplicated to generate a population, then the individuals in this population will be "mutated" (i.e., adding random variations to the enzyme concentrations). This process of selection and mutation iterates, and the rate of photosynthetic CO2 uptake rate gradually increases over generations. This process terminates when the rate of photosynthesis cannot be increased with more generations (Zhu et al., 2007). The final nitrogen distribution in the enzyme set is considered as the optimal nitrogen distribution (Figure 3).
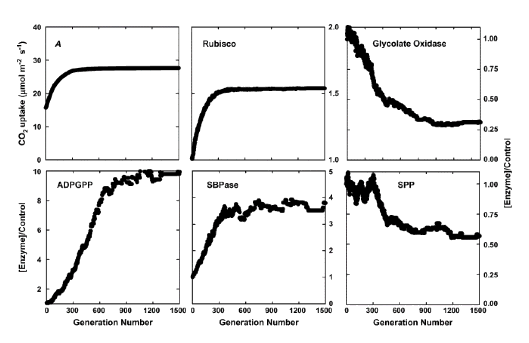
Figure 3. Selection of the optimal partitioning of resources between the enzymes of carbon metabolism to maximize light-saturated photosynthetic rate. A, increase in light-saturated photosynthetic rate over 1,500 generations of selection using an evolutionary algorithm. B to F show the changes in the amounts of five of these enzymes relative to their initial values over these 1,500 generations. Selection was at light saturation, and a Ci of 280 μmol mol-1.
Abbreviations:
A: photosynthetic CO2 uptake rate
ADPGPP: ADP glucose pyrophosphorylase
SBPase: sedoheptulose-l,7-bisphosphatase
SPP: sucrose phosphate phosphatase
FBPase: fructose-2,6-bisphosphatase.
From Zhu et al. (2007).
Once the optimal nitrogen distributions are identified, we can use it to calculate the demand of increase for each enzyme,
Demand[i] = [Enzyme[i]_opt]/ [Enzyme[i]_initial] …. (6)
Where [Enzyme[i]_opt] represents the optimal nitrogen concentration and [Enzyme[i]_initial] represents the initial nitrogen concentration. If the demand for an enzyme is higher than 1, the enzyme activity needs to be increased; otherwise, the enzyme activity needs to be dropped to free nitrogen for the synthesis of other enzymes to gain the optimal CO2 uptake rate (Zhu et al., 2007). Using this approach, we showed that Rubisco, SBPase and FBPase need to be increased for a higher photosynthetic CO2 rate (Zhu et al., 2007). Furthermore, an increase in sink capacity, i.e., the capacity to consume the triose phosphate (PGA, or dihydroxyacetone phosphate, or glyceraldehyde 3-phosphate) through the synthesis of starch, sucrose, or other macromolecules. The nitrogen required to increase activities of these enzymes is predicted to be reallocated from the photorespiratory pathway (Zhu et al., 2007). SBPase, one of the enzymes identified to be increased to gain higher photosynthesis, has been over-expressed in tobacco, which led to higher photosynthesis and biomass production (Lefebvre et al., 2005), demonstrating that combining evolutionary algorithm with systems models can identify potential engineering targets for higher photosynthesis.
Another approach to identify targets to engineer is metabolic control analysis (MCA) via the calculation of the flux control coefficient (Fell 1997). Both MCA and the evolutionary algorithm provide engineering targets; however, there are fundamental differences between these two approaches. The flux control coefficient of an enzyme represents the control of this enzyme over certain flux, assuming all other enzyme levels are not changed, i.e., this coefficient represents a local view of the control of this enzyme over the system flux. On the other hand, evolutionary algorithm identifies the optimal distribution of all the enzymes in the metabolism by simultaneously changing all the enzyme concentrations. Therefore, theoretically, the evolutionary algorithm can identify targets for higher photosynthesis from a more global view of the system.
iii) Why photosynthesis, after millions of years of evolution, has not evolved an optimal photosynthetic rate?
The combination of evolutionary algorithm with systems models provides a feasible and efficient mechanism to identify the optimal photosynthetic apparatus. One philosophical question people may ask is: after millions of years of evolution, why have plants not evolved an optimal photosynthetic apparatus? There are a few possible reasons. First, evolution selects survival and fecundity, not productivity. To ensure survival under stress conditions, a certain amount of resources, such as nitrogen, is invested in protective mechanisms at the expense of photosynthetic efficiency. For example, we have demonstrated that nitrogen is over-invested to the photorespiratory pathway (Zhu et al., 2007). This over investment, however, is critical for the survival of plants under extremely hot and draught conditions. Though such conditions are rare, maybe once every few hundred years, they might be frequent enough to completely eliminate plants without such protective mechanisms (Zhu et al., 2007). Secondly, global climate change is another factor. The ambient atmospheric CO2 concentration has been around 280 ppm for the past 25 million years (Barnola et al., 1999), before the rapid increase in the CO2 concentration after the Industrial Revolution. The current photosynthetic carbon metabolism, e.g., higher investment in the photorespiratory pathway, might represent an optimal nitrogen allocation for the preindustrial revolution CO2 levels (Zhu et al., 2007). We have previously demonstrated that one of the critical enzymes in photosynthesis, Rubisco, is indeed optimized for a higher CO2 uptake at an atmospheric CO2 concentration of 280 ppm (Zhu et al., 2004). Two more subtle reasons might also be responsible for the current non-optimal nitrogen allocation in photosynthetic carbon metabolism. The sub-optimal investment of SBPase might be related to the role of SBPase as a controlling point in photosynthetic carbon metabolism; while the over-investment of enzymes in the photorespiratory pathway might also be due to the strict ratio between RuBP carboxylation and oxygenation for a given Rubisco specificity and atmospheric conditions (Zhu et al., 2007).
Other major applications of photosynthesis systems models
Dynamic systems models hold a variety of other applications besides identifying new approaches to engineer for higher productivity. These include:
First, systems models provide a direct link of genomic data to phenotypic data. The inputs of the systems model are the enzyme activities or protein contents, which can be obtained from either literature survey or proteomics. The outputs of systems models are metabolite concentrations, fluxes, and physiological parameters.
Second, systems model can be used to study the adaptive significance of molecular changes in photosynthetic apparatus to photosynthetic efficiency. Here the photosynthetic apparatus is defined as the various components (enzymes, electron transfer carriers, etc.) and interactions between different components in photosynthesis. As mentioned earlier, combining evolutionary or genetic algorithms with systems model provides an efficient way to identify the optimal photosynthetic apparatus under defined conditions. This difference between the optimal photosynthetic apparatus and the existing photosynthetic apparatus provides opportunities for us to engineer for higher productivity. This difference also suggests the adaptation significance of different properties of the photosynthetic apparatus.
Third, dynamic systems models can be used to test hypotheses regarding mechanisms underlying dynamic signals related to photosynthesis. We have used a systems model of the primary events around photosystem II to study the mechanistic basis of fluorescence induction curve recorded after shining a saturating light pulse (i.e., a short light pulse (<1s) that can close all photosynthesis II reaction centers) on dark adapted leaves (Zhu et al., 2005).
Fourth, systems model of photosynthesis can be used in ecophysiological crop simulation models to enable direct linkage from genome to ecosystem. The computer aided design of the integrated circuit (IC) played a critical role in the rapid development of new IC technologies. It is expected that a model able to link from genome to ecosystem directly can serve the same role. Although agricultural ecosystems models have been developed over the past half century, they still cannot directly predict crop performance from a crop's genome and its growth environment (Jones et al., 2003), though there are few recent efforts to use QTLs (i.e., stretches of DNA that are closely linked to genes that underlie a trait) in agro-ecosystem models. (Yin et al., 2004).
Developing an integrated model able to directly link genome to ecosystem is extremely challenging, since such a model not only has to mechanistically describe processes at various organizational levels, ranging from the ecosystem level, to canopy level, leaf and cellular level processes, but also has to describe changes in gene expression under different conditions and different developmental stages. Undoubtedly, developing such a model will take years of joint effort by the whole plant modeling community. Considering that photosynthesis is the basis of material and energy for plant growth and development, a detailed mechanistic model of photosynthesis is a critical component of such an integrated model. Integration of the model of photosynthetic carbon metabolism with agri-ecosystem models might be the first step towards realizing such an integrated genome-to-ecosystem model.
Literature:
Barnola, J.M., Raynaud, D., Lorius, C. & Barkov, N.I. Historical CO2 record from the Vostok ice core. In Trends: A compendium of Data on Global Change. Carbon dioxide information analysis center, Oak Ridge National laboratory, Department of Energy, Oak Ridge, TN, U.S.A. (1999).
Evans L.T. Crop Evolution, Adaptation and Yield. CUP, Cambridge. (1993)
Fell, D.A. Understanding the control of metabolism. Portland Press, London (1997).
Jones, J.W., Hoogenboom, G., Porter, C.H., Boote, K.J., Batchelor, W.D., Hunt, L.A., Wilkens, P.W., Singh, U., Gijsman, A.J., Ritchie, J.T. The DSSAT cropping system model. European Journal Of Agronomy 18, 235-265 (2003).
Lefebvre, S., Lawson, T., Zakhleniuk, O.V., Lloyd, J.C. & Raines, C.A. Increased sedoheptulose-1,7-bisphosphatase activity in transgenic tobacco plants stimulates photosynthesis and growth from an early stage in development. Plant Physiol. 138, 451-460 (2005).
Long, S.P., Zhu, X.G., Naidu, S.L. & Ort, D.R. Can improvement in photosynthesis increase crop yields? Plant Cell Environ. 29, 315-330 (2006).
Long S.P., Ainsworth E.A., Rogers A. and Ort D.R. Rising atmospheric carbon dioxide: plants face their future. Annual Reviews of Plant Biology, 55, 591-628 (2004).
Monteith, J.L. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. London 281, 277-294 (1977).
Roberts M.J., Long S.P., Tieszen L.L. and Beadle C.L. Measurement of plant biomass and net primary production of herbaceous vegetation. In: Photosynthesis and Production in a Changing Environment: A Field and Laboratory Manual (eds, D.O. Hall, J.M.O. Scurlock, H.R. Bolhàr-Nordenkampf, R.C. Leegood, and S.P. Long), pp. 1-21. Chapman & Hall, London (1993).
Yin, X.Y., Struik, P.C. & Kropff, M.J. Role of crop physiology in predicting gene-to-phenotype relationships. Trends Plant Sci. 9, 426-432 (2004).
Zhu, X.-G., Portis Jr., A.R. & Long, S.P. Would transformation of C3 crop plants with foreign Rubisco increase productivity? A computational analysis extrapolating from kinetic properties to canopy photosynthesis. Plant Cell Environ. 27, 155-165 (2004).
Zhu, X.-G. Computational Approaches to Guiding Biotechnological Improvement of Crop Photosynthetic Efficiency. Ph.D. thesis, the University of Illinois. Urbana, IL. (2004).
Zhu, X.-G., Govindjee, Baker, N.R., deSturler, E., Ort, D.R., Long, S.P. Chlorophyll a fluorescence induction kinetics in leaves predicted from a model describing each discrete set of excitation energy and electron transfer associated with photosystem II. Planta 223, 114-133 (2005).
Zhu, X.-G., de Sturler, E. & Long, S.P. Optimizing the distribution of resources between enzymes of carbon metabolism can dramatically increase photosynthetic rate: A numerical simulation using an evolutionary algorithm. Plant Physiol. 145, 513-526 (2007).
Zhu, X.-G., Long, S.P. & Ort, D.R. What is the maximum efficiency with which photosynthesis can convert solar energy into biomass? Trends in Biotechnology 19, 153-159 (2008).
8/17/08